My Secret Rainbow

线性回归中的最小二乘法和梯度下降法比较

为什么要比较这两种方法呢？很多人可能不知道，我先简单的介绍一下

机器学习有两种，一种是监督学习，另一种是非监督学习。监督学习就是我告诉计算机你把班上同学分个类，分类标准是按照性别，男生和女生；非监督分类就是告诉计算机你自己去把班上同学分个类吧，我不告诉你分类标准。

在监督学习中，如果我们面对的变量是连续型的变量就要用到回归

回归其实是非常容易理解，也非常实用的一种方法，很多经济类的学生在写论文的时候都会用到回归的方法。比方说，距离市中心的距离越近（距离为x），房价就越高（房价是y），可以得到一个y=kx+b的式子来大概的表示x和y之间的关系

不过，大部分的情况下是很多条件一起制约y的，不仅有离市中心的距离x₁，还有房子的新旧程度x₂等等条件，那么可以用到多元回归，一般式如下：

其中  是预测值

 是系数

 是自变量

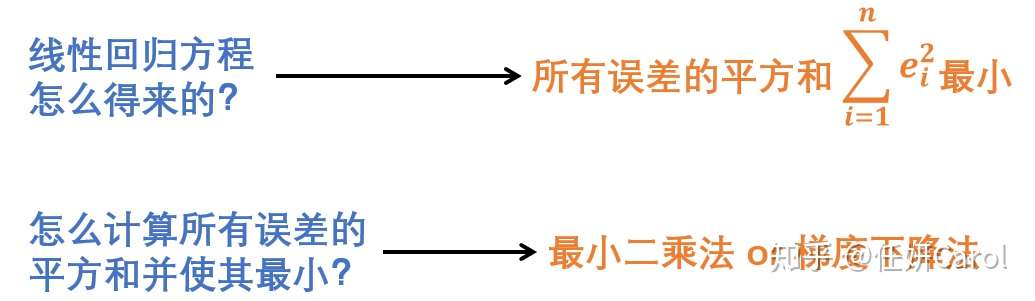
我们想要让这个方程拟合的非常好，那么就要使误差尽量小，评价误差小的方法就是所有误差的平方和最小

计算误差平方和最小的方法最常见的就是最小二乘法和梯度下降法

---

最小二乘法

最小二乘法是所有有数学思维的人面对这个问题第一想到的方法，最直接最不拐弯抹角的方法。就是求多元函数极值，这就是最小二乘法的思想！其实根本不用把最小二乘法想的多么高大上，不就是求极值嘛~

学过大学高等数学的人应该都知道求极值的方法：就是求偏导，然后使偏导为0，这就是最小二乘法整个的方法了，so easy啊~

最后使所有的偏导等于0

然后解这个方程组就可以得到各个系数的值了

---

梯度下降法

我们注意到最小二乘法最后一步要求p个方程组，是非常大的计算量，其实计算起来很难，因此我们就有了一种新的计算方法，就是梯度下降法，梯度下降法可以看作是 更简单的一种 求最小二乘法最后一步解方程 的方法

虽然只是针对最后一步的改变，不过为了计算简便，仍然要对前面的步骤做出一些改变：

recall上面的最小二乘法，我们有一个这样子的式子，就是所有误差的平方和：

假设有m个数据，2个系数（θ₀和θ₁），我们要对最小二乘法的Q稍加改变，变成代价函数J，虽然用不同的字母表示了，但是他们的含义是一模一样的啦~

前面的1/2m系数只是为了后面求导的时候，那个平方一求导不是要乘一个2嘛，然后和1/2m的2抵消就没了，变成如下：

然后θ₀和θ₁分别是这样子被计算出来的（其中:=为赋值的意思）：

这个计算方法其实理解起来比较难，那么我们先来看看这个J函数的图像吧，J函数是关于θ₀和θ₁的函数，因此是三维的，为了使J的值最小，也就是高度最。相当于一个人要下山，下到海平面最低的地方，在图中就是蓝色部分，那就是最低的地方

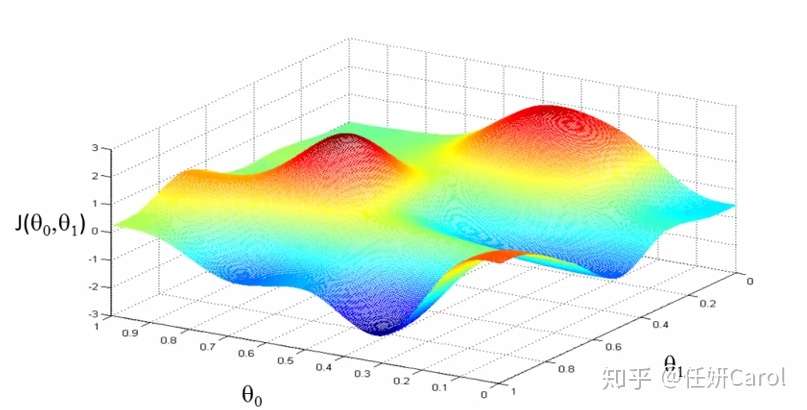
再想象这个人，要下到海平面最低的地方有很多条路啊，他可以绕着山头一圈一圈的下，像盘山公路一样（但没有人这样下山的，要走的距离也太长了8），最省力的方法就是按照梯度的方向下山，如图所示：

梯度：梯度是一个向量，梯度的方向就是最快下山，或者说沿着变化率最大的那个方向

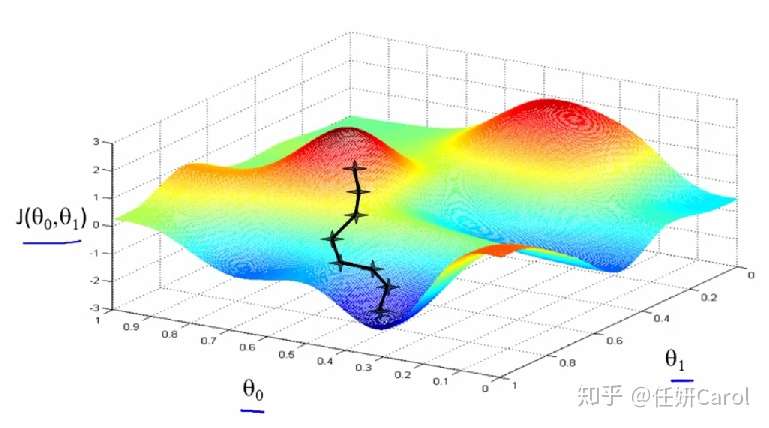
我们再来看一下

这个一个反复迭代的式子，就是初始的时候，先找一个点（θ₀，θ₁）（可以随便找），然后在这个点沿着梯度下降的方向，即这个向量的方向

然后α的意思就是下山的跨步，比方说我知道了我接下来哪个方下是最快下山的方向了，我一步子跨多大，跨的小容易娘炮，跨的大容易扯着蛋（开玩笑），跨的小容易走了很多步才到山脚下，跨的大容易把最地点那个坑 给一下子跨过去，因此要确定合适的α

每跨一步，就到了一个新的点，然后在这个点的基础上继续跨步，直到下到最低点（此时再想走的话就是上坡了，即偏导为正了），这就是一个反复迭代的过程

原文：https://zhuanlan.zhihu.com/p/55200001